Der goldene Schnitt und die (goldene) Fibonacci Spirale
sind faszinierende Konzepte, die Mathematik, Kunst, Natur und Ästhetik miteinander verbinden. Sie verkörpern ein harmonisches Verhältnis, das in vielen Bereichen als besonders ansprechend empfunden wird.
Siehe auch die Seite Drittelregel.
1. Der goldene Schnitt
Was ist der goldene Schnitt?
Der goldene Schnitt ist ein spezielles Verhältnis zwischen zwei Größen, bei dem das Verhältnis der kleineren Strecke (aa) zur größeren Strecke (bb) gleich dem Verhältnis der größeren Strecke (bb) zur Summe beider Strecken (a+ba + b) ist.
Mathematisch ausgedrückt: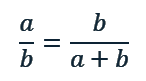
Mathematische Darstellung
Die Zahl, die dieses Verhältnis beschreibt, wird als Phi (φ) bezeichnet und beträgt näherungsweise 1,6180339887.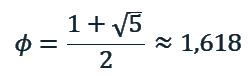
Dies bedeutet, dass die größere Strecke ungefähr 1,618-mal so lang ist wie die kleinere Strecke.
Visuelle Darstellung
Stellen wir uns eine Strecke vor, die in zwei Teile geteilt ist:
A------------B---------------------C
- AB ist die kleinere Strecke (aa).
- BC ist die größere Strecke (bb).
- Das Verhältnis
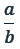entspricht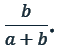 
2. Die goldene Fibonacci Spirale
Was ist die goldene Spirale?
Die goldene Spirale ist eine logarithmische Spirale, deren Wachstumsfaktor dem goldenen Schnitt entspricht. Sie wächst um den Faktor φ für jede 90-Grad-Drehung.
Konstruktion der goldenen Spirale
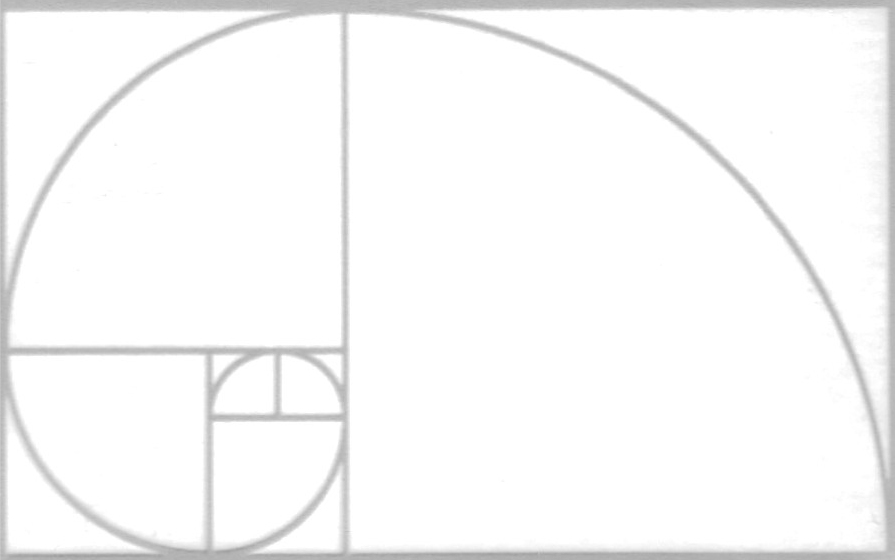
Die goldene Spirale kann konstruiert werden, indem man ein Rechteck im goldenen Schnitt in Quadrate und Rechtecke unterteilt und in jedes Quadrat einen Viertelkreis zeichnet.
Schritte zur Konstruktion:
- Zeichne ein goldenes Rechteck:
- Die Seitenlängen stehen im Verhältnis 1:ϕ.
- Unterteile das Rechteck:
- Erstelle ein Quadrat innerhalb des Rechtecks.
- Das verbleibende Rechteck ist wiederum ein goldenes Rechteck.
- Wiederhole die Unterteilung:
- Setze diesen Prozess mit den neuen goldenen Rechtecken fort.
- Zeichne die Spirale:
- Zeichne in jedes Quadrat einen Viertelkreis.
- Die Verbindung dieser Bögen ergibt die goldene Spirale.
Illustration der Fibonacci Spirale
3. Verbindung zur Fibonacci-Folge
Die Fibonacci-Folge ist eine Zahlenreihe, bei der jede Zahl die Summe der beiden vorherigen ist:
Das Verhältnis aufeinanderfolgender Fibonacci-Zahlen nähert sich mit zunehmender Größe dem goldenen Schnitt an: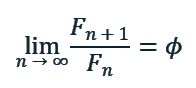
Dies zeigt die enge Verbindung zwischen der Fibonacci-Folge und dem goldenen Schnitt.
4. Vorkommen in der Natur
Der goldene Schnitt und die goldene Spirale sind in vielen natürlichen Strukturen zu finden:
- Schneckenhäuser: Die Wachstumsform vieler Muscheln und Schnecken folgt einer logarithmischen Spirale.
- Sonnenblumen: Die Anordnung der Samen bildet Spiralmuster, die auf Fibonacci-Zahlen basieren.
- Zapfen und Ananas: Die Schuppen sind in Spiralen angeordnet, deren Anzahl Fibonacci-Zahlen entspricht.
- Galaxien: Einige Spiralgalaxien, wie die Milchstraße, zeigen Arme, die der goldenen Spirale ähneln.
5. Anwendungen in Kunst und Architektur
Kunst
- Leonardo da Vinci nutzte den goldenen Schnitt in Werken wie dem Vitruvianischen Menschen und dem Abendmahl.
- Salvador Dalí integrierte in seinem Gemälde "Das Abendmahl" bewusst den goldenen Schnitt in die Komposition.
Architektur
- Parthenon in Athen: Es wird vermutet, dass die Proportionen des Tempels auf dem goldenen Schnitt basieren.
- Kathedrale von Notre-Dame: Elemente ihres Designs entsprechen dem goldenen Verhältnis.
Design
- Logo-Gestaltung: Unternehmen wie Twitter nutzen den goldenen Schnitt bei der Gestaltung ihres Logos.
- Fotografie: Kompositionsrichtlinien wie die goldene Spirale helfen Fotografen, harmonische Bilder zu erstellen.
6. Der goldene Schnitt in der Fotografie
Kompositionstechniken
- Goldene Spirale: Platziere das Hauptmotiv entlang der Spirale, um den Blick des Betrachters natürlich durch das Bild zu führen.
- Goldenes Rechteck: Nutze die Proportionen des goldenen Schnitts, um den Bildausschnitt zu bestimmen.
Vergleich zur Drittel-Regel
Während die Drittel-Regel das Bild in neun gleiche Teile teilt, bietet der goldene Schnitt eine etwas andere Aufteilung, die viele als natürlicher und angenehmer empfinden.
Interessante Anekdote
Der geheimnisvolle Kaninchen-Wachstum: Leonardo Fibonacci stellte im 13. Jahrhundert ein Gedankenexperiment über die Vermehrung von Kaninchen auf. Dieses führte zur Fibonacci-Folge, welche die Verbindung zum goldenen Schnitt offenbarte. Dieses einfache Szenario hat weitreichende Auswirkungen auf Mathematik und Naturwissenschaften gehabt!
Weiterführende Gedanken
Der goldene Schnitt zeigt, wie eng Mathematik und Ästhetik miteinander verwoben sind. Er bietet Einblicke in die natürliche Ordnung und dient als Werkzeug für Künstler, Architekten und Designer, um Harmonie und Balance zu erreichen.
Bildquelle [3]